[Shader Library] Noise and Pseudo Random Number Generator in GLSL

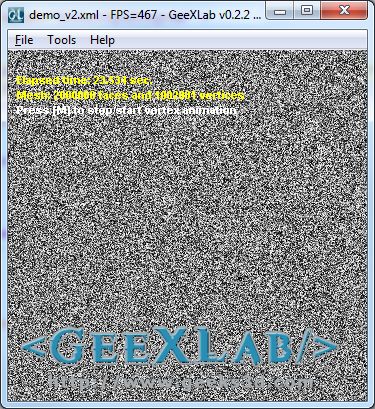
The noise generator used to deform a plane made up of 2’000’000 faces and 1’002’001 vertices

Here is an useful piece of GLSL code: a noise generator and its core function: a pseudo random number generator. I found this code in one of the Shader Toy demos (iq is really a GLSL wizzard!). I quickly extracted the interesting functions and tested them with GeeXLab.

The nice thing with this pseudo random generator is that it is only based on mathematic tricks. Actually the core of this random number generator relies on a LFSR (linear feedback shift register) generator. LFSR requires bits manipulation with operators like >>, <<>>, ^ or &. VirtualDub’s developer talks about LFSR in this post.

In GLSL, bitwise operators are provided by the GL_EXT_gpu_shader4 extension. According to Geeks3D’s OpenGL extensions DB, GL_EXT_gpu_shader4 is supported from Catalyst 8.10 for Radeon cards and from ages on NVIDIA boards.

Here is an excerpt from the GL_EXT_gpu_shader4 spec related to bitwise operators:

This extension provides a set of new features to the OpenGL Shading Language and related APIs to support capabilities of new hardware. In particular, this extension provides the following functionality:
– Full signed integer and unsigned integer support in the OpenGL Shading Language:
– Integer bitwise operators are now enabled.

I coded with GeeXLab a simple demo: a mesh plane is deformed using this noise generator:

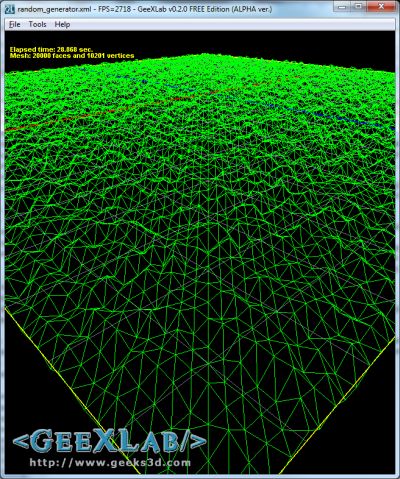
demo_v1.xml – the noise generator deforming a plane made up of 20,000 faces and 10,201 vertices (100×100 segments)

demo_v2.xml – the noise generator used in the vertex and pixel shader on a 1000×1000-segment plane

You can play with these demos in GeeXlab. Just download the demo pack here:
[download#160#image]

Just launch GeeXLab and drop demo source code in. The source code is localized in the demo_v1.xml or demo_v2.xml or demo_v3.xml files. The shortcut [Ctrl+R] in GeeXLab allows to reload the demo once you have modified the source code.

You can stop/start the deformation animation by hitting the SPACE key.

The second demo (demo_v2.xml) uses the random number generator in both vertex and pixel shaders with a plane made up of 1000×1000 segments: 2000000 faces and 1002001 vertices.

Some stats for the demo_v2.xml and for a GeForce GTX 460 + R258.96:

• 800×600 windowed, framerate: 92 FPS, CPU usage: 99%
• 1440×900 windowed, framerate: 70 FPS, CPU usage: 99%

Now the GLSL random number generator code that will allows us to get the noise3f() function:

[Vertex_Shader]
#extension GL_EXT_gpu_shader4: enable

uniform float time;

int LFSR_Rand_Gen(in int n)
{
  // <<, ^ and & require GL_EXT_gpu_shader4.
  n = (n << 13) ^ n; 
  return (n * (n*n*15731+789221) + 1376312589) & 0x7fffffff;
}

float LFSR_Rand_Gen_f( in int n )
{
  return float(LFSR_Rand_Gen(n));
}

float noise3f(in vec3 p)
{
  ivec3 ip = ivec3(floor(p));
  vec3 u = fract(p);
  u = u*u*(3.0-2.0*u);

  int n = ip.x + ip.y*57 + ip.z*113;

  float res = mix(mix(mix(LFSR_Rand_Gen_f(n+(0+57*0+113*0)),
                          LFSR_Rand_Gen_f(n+(1+57*0+113*0)),u.x),
                      mix(LFSR_Rand_Gen_f(n+(0+57*1+113*0)),
                          LFSR_Rand_Gen_f(n+(1+57*1+113*0)),u.x),u.y),
                 mix(mix(LFSR_Rand_Gen_f(n+(0+57*0+113*1)),
                          LFSR_Rand_Gen_f(n+(1+57*0+113*1)),u.x),
                      mix(LFSR_Rand_Gen_f(n+(0+57*1+113*1)),
                          LFSR_Rand_Gen_f(n+(1+57*1+113*1)),u.x),u.y),u.z);

  return 1.0 - res*(1.0/1073741824.0);
}

void main()
{	
  float disp = noise3f(gl_Vertex.xyz);
  vec3 P = gl_Vertex.xyz + (gl_Normal * disp * 2.0 * sin(time * 2.0));
  gl_Position = gl_ModelViewProjectionMatrix * vec4(P, 1.0);
}

[Pixel_Shader]
uniform vec4 color;
void main(void)
{
  gl_FragColor = color;
}

This shader is now part of Geeks3D’s shaders library

All demos have been successfully tested on a GeForce GTX 460 (R258.96) and on a Radeon HD 5770 (Catalyst 10.8).

Another pseudo random number generator based on the previous and returning normalized values (author: iq / rgba):

float rnd(vec2 x)
{
    int n = int(x.x * 40.0 + x.y * 6400.0);
    n = (n << 13) ^ n;
    return 1.0 - float( (n * (n * n * 15731 + 789221) + \
             1376312589) & 0x7fffffff) / 1073741824.0;
}

This cool noise3f() function is useful for many effects like this one: the generation of a Worm-Lava-Texture I discovered in the Making of Ergon 4k PC Intro.

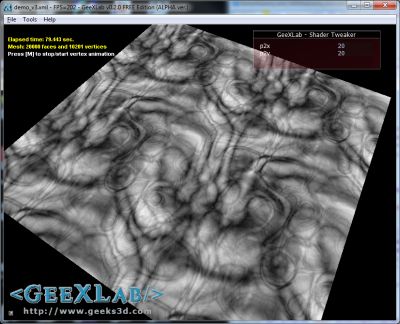
demo_v3.xml – Worm lava shader texture in GLSL

Here is the pixel shader. The complete source code is loalized in the demo_v3.xml.

#extension GL_EXT_gpu_shader4: enable

int LFSR_Rand_Gen(in int n)
{ ... }

float LFSR_Rand_Gen_f( in int n )
{ ... }

float noise3f(in vec3 p)
{ ... }

#define ty(x,y) (pow(.5+sin((x)*y*6.2831)/2.0,2.0)-.5)
#define t2(x,y) \
 ty(y + 2.0*ty(x+2.0*noise3f(vec3(cos((x)/3.0)+x,y,(x)*.1)),.3),.7)
#define tx(x,y,a,d) \
  ((t2(x, y) * (a - x) * (d - y) + \
   t2(x - a, y) * x * (d - y) + t2(x, y - d) * (a - x) * y + \
   t2(x - a, y - d) * x * y) / (a * d))
	 
vec4 fx(vec2 x)
{
  float a=0.0,d=32.0;
  // Modified FBM functions to generate a blob texture
  for(;d>=1.0;d/=2.0)
    a += abs(tx(x.x*2.0*d, x.y*2.0*d, 2.0*d, 2.0*d)/(2.0*d));
  return vec4(a*2.0);  
}

uniform vec4 color;
uniform float time;
uniform vec2 p2;

void main(void)
{
  vec2 uv = gl_TexCoord[0].xy * p2;
  uv -= floor(uv);
  gl_FragColor = fx(uv);
  gl_FragColor.a = 1.0;
}

p2 is an unifom vec2 I used to scale the texture coordinates. It’s controled from the demo via a tweak bar.